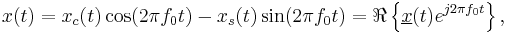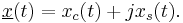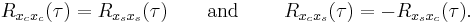Random modulation
In the theories of modulation and of stochastic processes, random modulation is the creation of a new signal from two other signals by the process of quadrature amplitude modulation. In particular, the two signals are considered as being random processes. For applications, the two original signals need have a limited frequency range, and these are used to modulate a third sinusoidal (carrier) signal whose frequency is above the range of frequencies contained in the original signals.
Details
The random modulation procedure starts with two stochastic baseband signals, 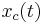 and
and 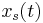 , whose frequency spectrum is non-zero only for
, whose frequency spectrum is non-zero only for ![f \in [-B/2,B/2]](/2012-wikipedia_en_all_nopic_01_2012/I/9894f7825045a5697e33fb64e235543d.png) . It applies quadrature modulation to combine these with a carrier frequency
. It applies quadrature modulation to combine these with a carrier frequency 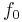 (with
(with 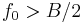 ) to form the signal
) to form the signal 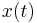 given by
given by
where 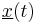 is the equivalent baseband representation of the modulated signal
is the equivalent baseband representation of the modulated signal 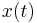
In the following it is assumed that 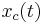 and
and 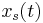 are two real jointly wide sense stationary processes. It can be shown that the new signal
are two real jointly wide sense stationary processes. It can be shown that the new signal 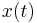 is wide sense stationary if and only if
is wide sense stationary if and only if 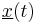 is circular complex, i.e. if and only if
is circular complex, i.e. if and only if 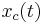 and
and 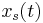 are such that
are such that
Bibliography
- (English)Papoulis, Athanasios; Pillai, S. Unnikrishna (2002). "Random walks and other applications". Probability, random variables and stochastic processes (4th ed.). McGraw-Hill Higher Education. pp. 463–473.
- (Italian)Scarano, Gaetano (2009). Segnali, Processi Aleatori, Stima. Centro Stampa d'Ateneo.
- Papoulis, A. (1983). "Random modulation: A review". IEEE Transactions on Acoustics, Speech, and Signal Processing 31: 96–35. doi:10.1109/TASSP.1983.1164046.